Implementing a 2 3 4 Tree in C++17¶
Implementation links:
2 3 4 Trees a Visual Introduction is an excellent tutorial with an animantion of how 2 3 4 algorithms work.
Balanced Search Trees has excellent slides and pseudocode of 2-3 and 2-3-4 trees.
B Tress and 2 3 4 Trees has a very good explanation with ilustrative examples.
2-3-4 Trees at Algorithm Tutor lists all cases for delete, including how root special case.
Deleting an entry from the (2,4)-tree has compelete Java delete code.
This link has an code and illustration of insertion.
General Description of a 2-3-4 Tree¶
How Insertion and Removal Algorithms Maintain a Balanced 2 3 4 Tree¶
Insertion¶
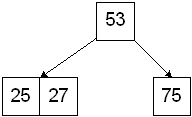
The insert algorithm is based on the this description of B-Trees and 2-3-4 Trees. New keys are inserted at leaf nodes. If the leaf is a 4-node, it is first be split into two 2-nodes: one will hold the left key, the other the right key, while the middle key pushed up into the parent. Take, for example, an int tree that has a 4-node root as its only node, if we insert 25,
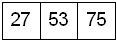
Figure: 4-node root to be split¶
the root will be split into two 2-nodes. A new root will be created containing the middle key, and 25 will be inserted into the left 2-node.
Below we insert 73 into this tree of height two.
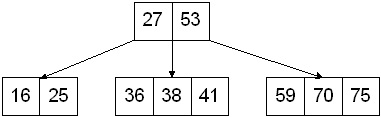
Figure: 4-node [59, 70, 75] needs to be split¶
Following the split, the tree looks like this:
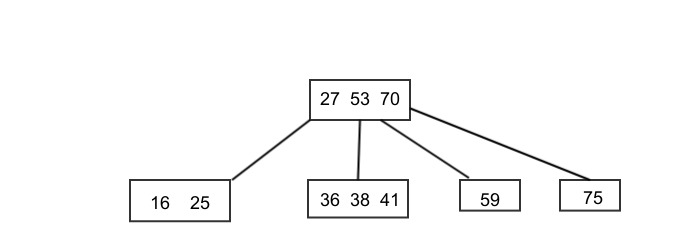
Figure: 4-node split into two 2-nodes¶
And after insertion:
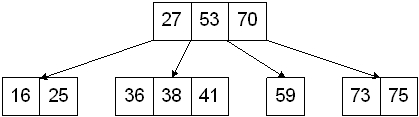
Figure: Tree after 73 inserted into leaf node¶
When a node is split and the parent also is a 4-node, split recurses. If it reaches a 4-node root, a new root is added above the current root, and the recursion terminates. An alternate split strategy is to automatically splits all 4-nodes encountered aduring the search for the insertion leaf node.
Deletion¶
For a leaf node, we simply delete the key. If the key is in an internal node, we swap the key with its in-order successor, and then we delete the swapped key from the leaf. To ensure deletion does not leave an empty node, 2-nodes are converted to 3- or 4-nodes as we descend the tree (except in the special case of the root). Doing so, preserves the ordering of the tree.
The in-order successor of an internal node’s key is found in the first key of the left-most leaf node of the internal node’s right subtree; for example, in this tree
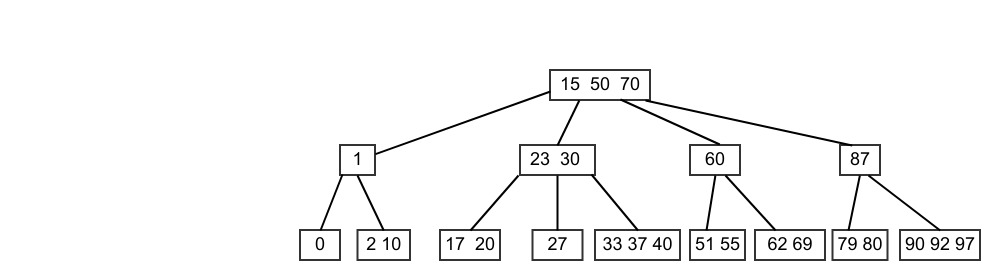
Figure: Internal Node in-order successor¶
the in-order successor of 23 is 27; of 50, 51; of 60, 62; and so on—all successors of these internal nodes are the first key in the left most leaf node of the right subtree.
There are two techniques for converting 2-nodes into 3-nodes as we descend the tree: 1.) “stealing” a key from a sibling and a parent(explained below), creating a 3-node; or 2.) fusing the node with a parent key and silbing key, creating a 4-node. We always attempt to barrow first, so we can fuse, if barrowing fails.
Case 1: Barrow a Key From Sibling
If an adjacent sibling of the 2-node is a 3- or 4-node, we can “steal” an key from the sibling. It is moved up to the parent, and a parent key is moved into the 2-node making it a 3-node. The children affected are transfered accordingly. For example, if 4 is to be deleted from this tree
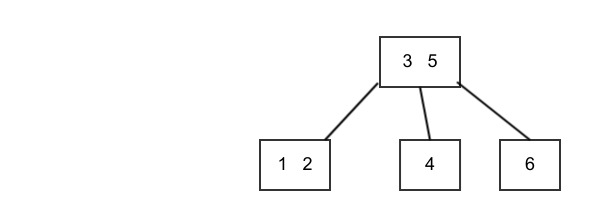
Figure: Delete from 4 from 2-node by barrowing¶
we barrow the 2 from the left sibling, move it into the parent, and we bring 3 down from the parent creating a 3-node.
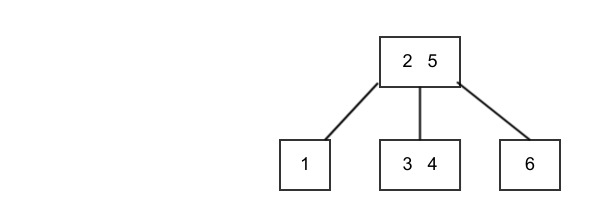
Figure: 2-node after barrowing¶
We then delete 4 from the leaf contain 3 and 4, we only need shift keys with the node. No new nodes are created or deleted, and the tree remains balanced.
Case 2: Fuse with Parent and Sibling
If each adjacent sibling (there are at most two) is a 2-node, we steal a key from the parent and from a sibling and fuse these two keys with the 2-node, creating a 4-node. The sibling is deleted, and its children adopted by the 4-node. The parent is down-sized. We know the parent will be a 3- or 4-node because we maintain the invariant that as we descend we eliminated the 2-nodes.
For example, say, we wish to delete 6 from our first example:

Figure: Delete from 6 from 2-node by fusing siblings¶
Since there a no 3- or 4-node siblings, we fuse the 2-node containing 4 into the 2-node containing 6, and we also bring down 5 from the parent, making the leaf node into a 4-node, from which we can delete 6:
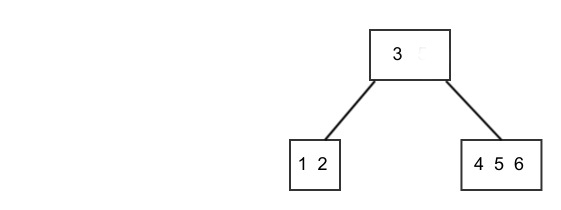
Figure: 2-node now a 4-node¶
Special Fuse Case: the root
If a 2-node has two 2-node children, the node is the root. We know this because this situation is always handled first as a special case, and once handled the root becomes a 4-node. If a child of the root must subsequently be converted from a 2-node, we know its parent, the root, is a 4-node. And if a child of this child, in turn, needs to be converted, its parent won’t not be a 2-node and similarly for all subsequent children.
Note that when a fusion occurs, the total number of nodes is decreased by one, but the tree again remains balanced.
Finally, if the key to be deleted is the largest key, there will be no in order successor; however, by applying the 2-node conversion technique above, we ensure that the tree will remain balanced.
Note
If the key is found in an internal node, the processes of finding its in order successor begins with the subtree rooted at the first child (to the right) that holds larger key(s). If this immediate child is a 2-node, it must be converted to a 3-node, but this conversion may also move the original key down into the converted 2-node. It may or may not move as a result of stealing a key from a sibling, but if it does it becomes the first key. If on the other hand a fusion happens, it becomes the 2nd key. This logic is in the function get_delete_successor().
Implementation of class tree234¶
The template class tree234 implements the 2 3 4 tree. unique_ptr<Node> manages the nodes of the tree. The root is also an instance of shared_ptr<Node>. Mention copy ctor and move ctor. And how this differs from shared_ptr<Node> implementation. This code is available on github.
#ifndef TREE234_H
#define TREE234_H
#include <utility>
#include <algorithm>
#include <stdexcept>
#include <algorithm>
#include <memory>
#include <array>
#include <queue>
#include <deque>
#include <stack>
#include <sstream>
#include <exception>
#include <iosfwd>
#include <string>
#include <iostream>
#include "value-type.h" // This header was taken from clang's STL implementation. It works like a union for the two
// types std::pair<Key, Value> and std::pair<const Key, Value>.
template<typename Key, typename Value> class tree234; // Forward declaration
template<typename Key, typename Value> class tree234 {
public:
// Container typedef's used by STL.
using key_type = Key;
using mapped_type = Value;
using value_type = __value_type<Key, Value>::value_type; // = std::pair<const Key, Value> within value_type.h
using difference_type = long int;
using pointer = value_type*;
using reference = value_type&;
class Node; // Forward reference.
class Node {
/*
Node depends on both of tree234's template parameters, Key and Value, so we make it a nested class.
*/
private:
friend class tree234<Key, Value>;
inline static const int MAX_KEYS;
enum class NodeType : int { two_node=1, three_node=2, four_node=3 };
int totalItems; /* If 1, two node; if 2, three node; if 3, four node. */
Node *parent; /* parent never owns the memory it points to. It is used to ease tree navigation. */
std::array<__value_type<Key, Value>, 3> keys_values; // Fix size of 3 __value_type<Key, Value>'s.
/*
* For 2-nodes, children[0] is left pointer and children[1] is right pointer.
* For 3-nodes, children[0] is left pointer, children[1] the middle pointer, and children[2] the right pointer.
* For 4-nodes, children[0] is left pointer, children[1] the left middle pointer, and children[2] is the right middle pointer,
* and children[3] is the right pointer.
*/
std::array<std::unique_ptr<Node>, 4> children; // Node owns the memory of the children it points to.
constexpr Node *getParent() noexcept { return parent; }
int getChildIndex() const noexcept; // Returns int value i such that parent->children[i] == this.
/*
* Returns either:
1. {true, Node * pnode, int index} -- if key is found. pnode->keys_values[index] == found_key
2. {false, Node * pnode, int index} -- if key is not found. pnode and index set to the next to key in next prospective node to search one level down in the tree.
*/
std::tuple<bool, typename tree234<Key, Value>::Node *, int> find(Key key) const noexcept;
int insert(const Key& key, const Value& value) noexcept;
void insert(__value_type<Key, Value>&& key_value, std::unique_ptr<Node>& newChild) noexcept;
__value_type<Key, Value> removeKeyValue(int index) noexcept;
value_type& get_value(int i) noexcept // simply helpers
{
return keys_values[i].__get_value();
}
const value_type& get_value(int i) const noexcept
{
return keys_values[i].__get_value();
}
// Takes ownership of unique_ptr<Node>, making it child number childNum.
void insertChild(int childNum, std::unique_ptr<Node>& pChild) noexcept;
void connectChild(int childNum, std::unique_ptr<Node>& child) noexcept;
/*
* Removes unique_ptr<Node> at child_index and shifts children to fill the gap. Returns unique_ptr<Node>.
*/
std::unique_ptr<Node> disconnectChild(int child_index) noexcept;
Node *make4Node() noexcept; // Called during a special case of remove() algorithm.
std::pair<bool, int> chooseSibling(int child_index) const noexcept;
public:
Node() noexcept;
~Node() // For debug purposes only
{
// std::cout << "~Node(): " << *this << std::endl;
}
Node(const Key& small, const Value& value, Node *in_parent=nullptr) noexcept : totalItems{1}, parent{in_parent}
{
keys_values[0] = {small, value};
// Note: This ctor implicitly set children to nullptr
}
Node(const Node& node) noexcept;
explicit Node(__value_type<Key, Value>&& key_value) noexcept;
Node(Node&&) = delete;
// This constructor is called by copy_tree()
Node(const std::array<value_type, 3>& lhs, Node *const lhs_parent, int lhs_totalItems) noexcept;
constexpr const Node *getParent() const noexcept;
constexpr int getTotalItems() const noexcept;
constexpr int get_lastkey_index() const noexcept { return getTotalItems() - 1; }
constexpr int getChildCount() const noexcept;
constexpr const Node *getRightMostChild() const noexcept { return children[getTotalItems()].get(); }
// Helps in debugging
void printKeys(std::ostream&);
constexpr const Key& key(int i) const noexcept
{
return keys_values[i].__get_value().first; // 'template<typename _Key, typename _Value> struct keys_values[i].__value_type' does not have members first and second.
}
int getIndexInParent() const;
constexpr bool isLeaf() const noexcept;
constexpr bool isTwoNode() const noexcept;
constexpr bool isThreeNode() const noexcept;
constexpr bool isFourNode() const noexcept;
constexpr bool isEmpty() const noexcept;
std::ostream& print(std::ostream& ostr) const noexcept;
friend std::ostream& operator<<(std::ostream& ostr, const Node& node234)
{
return node234.print(ostr);
}
std::ostream& debug_print(std::ostream& ostr) const noexcept;
}; // end class Tree<Key, Value>::Node
class NodeLevelOrderPrinter {
std::ostream& ostr;
int current_level;
int height;
std::ostream& (Node::*pmf)(std::ostream&) const noexcept;
void display_level(std::ostream& ostr, int level) const noexcept
{
ostr << "\n\n" << "current level = " << level << ' ';
// Provide some basic spacing to tree appearance.
std::size_t num = height - level + 1;
std::string str( num, ' ');
ostr << str;
}
public:
NodeLevelOrderPrinter (int height_in, std::ostream& (Node::*pmf_)(std::ostream&) const noexcept, std::ostream& ostr_in): ostr{ostr_in}, current_level{0}, height{height_in}, pmf{pmf_} {}
NodeLevelOrderPrinter (const NodeLevelOrderPrinter& lhs): ostr{lhs.ostr}, current_level{lhs.current_level}, height{lhs.height}, pmf{lhs.pmf} {}
void operator ()(const Node *pnode, int level)
{
// Did current_level change?
if (current_level != level) {
current_level = level;
display_level(ostr, level);
}
(pnode->*pmf)(std::cout);
std::cout << ' ' << std::flush;
}
};
private:
std::unique_ptr<Node> root;
int tree_size; // adjusted by insert(), remove(), operator=(const tree234...), move ctor
// Implementations of the public depth-frist traversal methods
template<typename Functor> void DoInOrderTraverse(Functor f, const Node *proot) const noexcept;
template<typename Functor> void DoPostOrderTraverse(Functor f, const Node *proot) const noexcept;
template<typename Functor> void DoPreOrderTraverse(Functor f, const Node *proot) const noexcept;
Node *split(Node *node, Key new_key) noexcept; // called during insert(Key key) to split 4-nodes when encountered.
// Called during remove(Key key)
bool remove(Node *location, Key key);
// Called during remove(Key key, Node *) to convert two-node to three- or four-node during descent of tree.
int convert2Node(Node *node, int child_index) noexcept;
// These methods are called by convert2Node()
// Returns converted Node, pnode, and child_index such that parent->children[child_index] == pnode
int make4Node(Node *parent, int node2_id, int sibling_id) noexcept;
int make3Node(Node *p2node, int child_index, int sibling_index) noexcept;
// Two subroutines of make3Node():
Node *leftRotation(Node *p2node, Node *psibling, Node *parent, int parent_key_index) noexcept;
Node *rightRotation(Node *p2node, Node *psibling, Node *parent, int parent_key_index) noexcept;
// Returns node with smallest value of tree whose root is 'root'
const Node *min(const Node* root) const noexcept;
const Node *max(const Node* root) const noexcept;
int height(const Node *pnode) const noexcept;
int depth(const Node *pnode) const noexcept;
bool isBalanced(const Node *pnode) const noexcept;
bool find(const Node *current, Key key) const noexcept;
std::tuple<bool, Node *, int> find_insert_node(Node *pnode, Key new_key) noexcept; // Called during insert
std::tuple<bool, typename tree234<Key, Value>::Node *, int> find_delete_node(Node *pcurrent, Key delete_key, int child_index=0) noexcept;
Node *get_successor_node(Node *pnode, int child_index) noexcept; // Called during remove()
std::tuple<Node *, int, Node *> get_delete_successor(Node *pdelete, Key delete_key, int delete_key_index) noexcept;
void destroy_subtree(std::unique_ptr<Node>& current) noexcept;
public:
using node_type = Node;
void debug() noexcept; // As an aid in writting any future debug code.
explicit tree234() noexcept : root{}, tree_size{0} { }
tree234(const tree234& lhs) noexcept;
tree234(tree234&& lhs) noexcept; // move constructor
tree234& operator=(const tree234& lhs) noexcept;
tree234& operator=(tree234&& lhs) noexcept; // move assignment
tree234(std::initializer_list<std::pair<Key, Value>> list) noexcept;
constexpr int size() const;
~tree234() //--= default;
{
destroy_subtree(root); // The default dtor is recursive
}
// Breadth-first traversal
template<typename Functor> void levelOrderTraverse(Functor f) const noexcept;
// Depth-first traversals
template<typename Functor> void inOrderTraverse(Functor f) const noexcept;
template<typename Functor> void iterativeInOrderTraverse(Functor f) const noexcept;
template<typename Functor> void postOrderTraverse(Functor f) const noexcept;
template<typename Functor> void preOrderTraverse(Functor f) const noexcept;
// Used during development and testing
template<typename Functor> void debug_dump(Functor f) noexcept;
bool find(Key key) const noexcept;
void insert(const Key& key, const Value &) noexcept;
void insert(const value_type& pair) noexcept { insert(pair.first, pair.second); }
bool remove(Key key);
void printlevelOrder(std::ostream&) const noexcept;
void debug_printlevelOrder(std::ostream& ostr) const noexcept;
void printInOrder(std::ostream&) const noexcept;
void printPreOrder(std::ostream&) const noexcept;
void printPostOrder(std::ostream&) const noexcept;
bool isEmpty() const noexcept;
int height() const noexcept;
bool isBalanced() const noexcept;
friend std::ostream& operator<<(std::ostream& ostr, const tree234<Key, Value>& tree)
{
tree.printlevelOrder(ostr);
return ostr;
}
// Bidirectional stl-compatible constant iterator
class iterator {
public:
using difference_type = std::ptrdiff_t;
using value_type = tree234<Key, Value>::value_type;
using reference = value_type&;
using pointer = value_type*;
using iterator_category = std::bidirectional_iterator_tag;
friend class tree234<Key, Value>;
private:
tree234<Key, Value>& tree;
const Node *current;
const Node *cursor; // points to "current" node.
int key_index;
std::stack<int> child_indexes;
std::pair<const typename tree234<Key, Value>::Node *, int> findLeftChildAncestor() noexcept;
iterator& increment() noexcept;
iterator& decrement() noexcept;
iterator(tree234<Key, Value>& lhs, int i); // called by end()
std::pair<const Node *, int> getSuccessor(const Node *current, int key_index) noexcept;
std::pair<const Node *, int> getPredecessor(const Node *current, int key_index) noexcept;
// Subroutines of the two methods above.
std::pair<const Node *, int> getInternalNodeSuccessor(const Node *pnode, int index_of_key) noexcept;
std::pair<const Node *, int> getInternalNodePredecessor(const Node *pnode, int index_of_key) noexcept;
std::pair<const Node *, int> getLeafNodeSuccessor(const Node *pnode, int key_index);
std::pair<const Node *, int> getLeafNodePredecessor(const Node *pnode, int key_index);
const Node *get_min() noexcept;
const Node *get_max() noexcept;
void push(int child_index)
{
child_indexes.push(child_index);
}
int pop()
{
if (child_indexes.empty()) {
throw(std::logic_error("iterator popping empty stack"));
}
auto i = child_indexes.top();
child_indexes.pop();
return i;
}
constexpr reference dereference() const noexcept
{
auto non_const_current = const_cast<Node *>(current);
return non_const_current->keys_values[key_index].__get_value();
}
public:
explicit iterator(tree234<Key, Value>&);
iterator(const iterator& lhs) = default;
iterator(iterator&& lhs);
bool operator==(const iterator& lhs) const;
constexpr bool operator!=(const iterator& lhs) const { return !operator==(lhs); }
iterator& operator++() noexcept
{
increment();
return *this;
}
iterator operator++(int) noexcept
{
iterator tmp(*this);
increment();
return tmp;
}
iterator& operator--() noexcept
{
decrement();
return *this;
}
iterator operator--(int) noexcept
{
iterator tmp(*this);
decrement();
return tmp;
}
reference operator*() const noexcept
{
return dereference();
}
pointer operator->() const noexcept
{
return const_cast<const pointer>( &(dereference()) );
}
friend std::ostream& operator<<(std::ostream& ostr, const iterator& iter)
{
return iter.print(ostr);
}
std::ostream& print(std::ostream& ostr) const noexcept;
};
class const_iterator {
public:
using difference_type = std::ptrdiff_t;
using value_type = tree234<Key, Value>::value_type;
using reference = const tree234<Key, Value>::value_type&;
using pointer = const tree234<Key, Value>::value_type*;
using iterator_category = std::bidirectional_iterator_tag;
friend class tree234<Key, Value>;
private:
iterator iter;
const_iterator(const tree234<Key, Value>& lhs, int i); // called by end()
reference dereference() const noexcept
{
return iter.cursor->keys_values[iter.key_index].__get_value();
}
public:
explicit const_iterator(const tree234<Key, Value>& lhs);
const_iterator(const const_iterator& lhs);
const_iterator(const_iterator&& lhs);
// Provides the implicit conversion from iterator to const_iterator
const_iterator(const typename tree234<Key, Value>::iterator& lhs);
bool operator==(const const_iterator& lhs) const;
bool operator!=(const const_iterator& lhs) const;
reference operator*() const noexcept
{
return dereference();
}
pointer operator->() const noexcept
{
return &this->operator*();
}
const_iterator& operator++() noexcept
{
iter.increment();
return *this;
}
const_iterator operator++(int) noexcept
{
const_iterator tmp(*this);
iter.increment();
return tmp;
}
const_iterator& operator--() noexcept
{
iter.decrement();
return *this;
}
const_iterator operator--(int) noexcept
{
const_iterator tmp(*this);
iter.decrement();
return tmp;
}
friend std::ostream& operator<<(std::ostream& ostr, const const_iterator& it)
{
return it.iter.print(ostr);
}
};
iterator begin() noexcept;
iterator end() noexcept;
const_iterator begin() const noexcept;
const_iterator end() const noexcept;
using reverse_iterator = std::reverse_iterator<iterator>;
using const_reverse_iterator = std::reverse_iterator<const_iterator>;
reverse_iterator rbegin() noexcept;
reverse_iterator rend() noexcept;
const_reverse_iterator rbegin() const noexcept;
const_reverse_iterator rend() const noexcept;
};
template<class Key, class Value> inline bool tree234<Key, Value>::isEmpty() const noexcept
{
return !root ? true : false;
}
/*
* Node constructors. Note: While all children are initialized to nullptr, this is not really necessary.
* Instead you can simply set children[0] = nullptr, since a Node is a leaf if and only if children[0] == nullptr.
*/
template<typename Key, typename Value> inline tree234<Key, Value>::Node::Node() noexcept : parent{nullptr}, totalItems{0}
{
// Note: Default member construction used for keys_values and children
}
template<typename Key, typename Value> inline tree234<Key, Value>::Node::Node(__value_type<Key, Value>&& key_value) noexcept : totalItems{1}, parent{nullptr}
{
keys_values[0] = std::move(key_value);
}
template<typename Key, typename Value> inline tree234<Key, Value>::Node::Node(const Node& lhs) noexcept : totalItems{lhs.totalItems}, keys_values{lhs.keys_values}
{
if (!lhs.parent) // If lhs is the root, then set parent to nullptr.
parent = nullptr;
if (lhs.isLeaf()) { // A leaf node's children are all nullptr
for (auto i = 0; i < lhs.getChildCount(); ++i)
children[i] = nullptr;
} else {
// The make_unique<Node> calls recursively invoke this constructor again and again util the entire tree rooted at lhs is duplicated.
// lhs being copied.
for (auto i = 0; i < lhs.getChildCount(); ++i) {
children[i] = std::make_unique<Node>(*lhs.children[i]);
children[i]->parent = this;
}
}
}
template<class Key, class Value> std::ostream& tree234<Key, Value>::Node::print(std::ostream& ostr) const noexcept
{
ostr << "[";
if (getTotalItems() == 0) { // remove() situation when merge2Nodes() is called
ostr << "empty";
} else {
for (auto i = 0; i < getTotalItems(); ++i) {
const auto& pair = keys_values[i].__get_value();
ostr << pair.first; /* << ", " << pair.second; */ // or to print both keys and values do: ostr << keys_values[i];
if (i + 1 == getTotalItems()) {
continue;
} else {
ostr << ", ";
}
}
}
ostr << "]";
return ostr;
}
template<class Key, class Value> int tree234<Key, Value>::Node::getIndexInParent() const
{
for (int child_index = 0; child_index <= parent->getTotalItems(); ++child_index) { // Check the address of each of the children of the parent with the address of "this".
if (this == parent->children[child_index].get()) {
return child_index;
}
}
throw std::logic_error("Cannot find the parent child index of the node. The node may be the tree's root or the invariant may have been violated.");
}
/*
* Does a post order tree traversal, using recursion and deleting nodes as they are visited.
*/
template<typename Key, typename Value> inline tree234<Key, Value>::tree234(const tree234<Key, Value>& lhs) noexcept
{
// Node(const Node&) will copy the entire tree rooted at lhs.get().
root = std::make_unique<Node>(*lhs.root);
tree_size = lhs.tree_size;
}
// Node(Node&&) will copy the entire tree rooted at lhs.get().
template<typename Key, typename Value> inline tree234<Key, Value>::tree234(tree234&& lhs) noexcept : root{std::move(lhs.root)}, tree_size{lhs.tree_size}
{
root->parent = nullptr;
lhs.tree_size = 0;
}
template<typename Key, typename Value> inline tree234<Key, Value>::tree234(std::initializer_list<std::pair<Key, Value>> il) noexcept : root(nullptr), tree_size{0}
{
for (auto&& [key, value]: il) {
insert(key, value);
}
}
/*
*
* Pseudo code for getting the successor is from: http://ee.usc.edu/~redekopp/cs104/slides/L19_BalancedBST_23.pdf:
*
Finding the successor of a given node
-------------------------------------
Requires:
* 1. If position is beg, Node *current and key_index MUST point to first key in tree.
* 2. If position is end, Node *current and key_index MUST point to last key in tree.
*
* 3. If position is in_between, current and key_index does not point to either the first key in the tree or last key. If the tree has only one node,
* the state can only be in_between if the first node is a 3-node.
*
* Returns:
* pair<const Node *, int>, where pnode->key(key_index) is next in-order key.
* If the last key has already been visited, the pointer returned will be nullptr.
*
*/
template<class Key, class Value> std::pair<const typename tree234<Key, Value>::Node *, int> tree234<Key, Value>::iterator::getSuccessor(const Node *current, int key_index) noexcept
{
if (current->isLeaf()) { // If leaf node
const auto& root = tree.root;
if (current == root.get()) { // special case: current is root and root is a leaf
// If root has more than one value--it is not a 2-node--and key_index is not the right-most key/value pair in the node,
// return the index of the key immediately to the right.
if (!root->isTwoNode() && key_index != root->get_lastkey_index()) {
return {current, key_index + 1};
}
return {nullptr, 0}; // There is no successor because key_index is the right-most index.
} else
return getLeafNodeSuccessor(current, key_index);
} else { // else internal node successor
return getInternalNodeSuccessor(current, key_index);
}
}
/*
Requires: pnode is an internal node not a leaf node.
Returns: pointer to successor of internal node.
*/
template<class Key, class Value> std::pair<const typename tree234<Key, Value>::Node *, int> tree234<Key, Value>::iterator::getInternalNodeSuccessor(const typename tree234<Key, Value>::Node *pnode, int key_index) noexcept
{
auto child_index = key_index + 1;
// Get first right subtree of pnode, and descend to its left most left node.
for (const Node *pcurrent = pnode->children[child_index].get(); pcurrent; pcurrent = pcurrent->children[child_index].get()) {
push(child_index);
pnode = pcurrent;
child_index = 0; // Set only after push(child_index)
}
return {pnode, 0};
}
/*
Requires: pnode is a leaf node other than the root.
*/
template<class Key, class Value> std::pair<const typename tree234<Key, Value>::Node *, int> tree234<Key, Value>::iterator::getLeafNodeSuccessor(const Node *pnode, int key_index)
{
const auto& root = tree.root;
// Handle the easy case: a 3- or 4-node in which key_index is not the right most value in the node.
if (!pnode->isTwoNode() && (pnode->get_lastkey_index()) != key_index) {
return {pnode, key_index + 1};
}
// Handle the harder case: pnode is a leaf node and pnode->keys_values[key_index] is the right-most key/value in this node.
// Get child_index such that parent->children[child_index] == pnode.
auto child_index = pop();
// Handle the case: pnode is the right-most child of its parent...
if (pnode->parent->children[child_index].get() == pnode->parent->getRightMostChild()) {
/*
pnode is a leaf node, and pnode is the right-most child of its parent, and key_index is the right-most index or last index into pnode->keys(). To find the successor, we need the first ancestor node that contains
a value great than current_key. To find this ancester, we ascend the tree until we encounter the first ancestor node that is not a right-most child of its parent, that is, where
ancester != ancestor->parent->getRightMostChild(). If the ancestor becomes equal to the root before this happens, there is no successor: pnode is the right most node in the tree and key_index is its right-most key.
*/
const Node *parent = pnode->parent;
// Ascend upward the parent pointer as long as the child continues to be the right most child (of its parent).
for(;child_index == parent->getTotalItems(); parent = pnode->parent) {
// If child is still the right most child, and if it is also the root, then, there is no successor. pnode holds the largest key in the tree.
if (parent == root.get()) {
return {nullptr, 0}; // To indicate "no-successor" we return the pair: {nullptr, 0}.
}
child_index = pop();
pnode = parent;
}
/*
We know that pnode now is NOT the right most child of its parent.
We need to ascertain the next index, next_index, such that parent->key(next_index) > current_key. We know 'pnode == parent->children[child_index]'. child_index is therefore
also the index of the successor key in the parent: successor-key == parent->key(child_index). We can see this by looking these possiblities. First, a 3-node.
If we ascende from the leaf node of the right-most subtree of key 5,then 36 is the successor, and 36 == parent->key(child_index)
[3, 36]
/ / \
/ / \
[1, 2] [4, 5] [47]
/ \ / | \ / \
and a 4-node can be viewed as three catenated 2-nodes in which the two middle child are shared
[2, 4, 36]
/ / \ \
[1] [3] [5] [37]
/ \ / \ / \ / \
Again, if ascend, say, the leaf of the right subtree root at key 3, then 4 is the successor; and if ascend, say, the leaf of the right subtree whose root is key 5, then 36 is the successor, and
36 = parent->key(child_index);
*/
return {parent, child_index};
} else { // Handle the case: pnode is not the right-most child of its parent.
/*
...else we know that pnode is NOT the right most child of its parent (and it is a leaf). We also know that key_index is the right most value of pnode (and in the case of a 2-node, key_index can only be zero, which is
also the "right-most" index).
We need to ascertain the next index, next_index, such that pnode->parent->key(next_index) > pnode->key(key_index). To determine next_index, we can view a 3-node as two catenated 2-nodes in which the the middle child is
shared between these two "2-nodes", like this
[3, 6]
/ \ / \
/ \ / \
[1, 2] [4, 5] [7]
and a 4-node can be viewed as three catenated 2-nodes in which the two middle child are shared
[2, 4, 6]
/ \ / \ / \
[1] [3] [5] [7]
If the leaft node is a 3- or 4-node, we already know (from the first if-test) that the current key is the last, current_key == pnode->get_lastkey_index(). So the we simply go up on level to find the in order successor.
We know pnode == parent->children[child_index]. child_index also is index of the successor key in the parent: successor-key == parent->key(child_index).
*/
if (child_index > static_cast<int>(Node::NodeType::four_node)) {
throw std::logic_error("child_index was not between 0 and 3 in getLeafNodeSuccessor()");
}
return {pnode->parent, child_index};
}
}
template<class Key, class Value> std::pair<const typename tree234<Key, Value>::Node *, int> tree234<Key, Value>::iterator::getPredecessor(const typename tree234<Key, Value>::Node *current, int key_index) noexcept
{
const auto& root = tree.root;
if (current->isLeaf()) { // If leaf node
if (current == root.get()) { // root is leaf
if (key_index != 0) {
return {current, key_index - 1};
}
return {nullptr, 0};
} else {
return getLeafNodePredecessor(current, key_index);
}
} else { // else internal node
return getInternalNodePredecessor(current, key_index);
}
}
template<class Key, class Value> std::pair<const typename tree234<Key, Value>::Node *, int> tree234<Key, Value>::iterator::getInternalNodePredecessor(\
const typename tree234<Key, Value>::Node *pnode, int key_index) noexcept
{
auto child_index = key_index;
for (const Node *pcurrent = pnode->children[key_index].get(); pcurrent; pcurrent = pcurrent->children[child_index].get()) {
push(child_index);
pnode = pcurrent;
child_index = pcurrent->getTotalItems(); // Must do after push()
}
return {pnode, pnode->totalItems - 1};
}
/*
Finding the predecessor of a given node
---------------------------------------
If left child exists, predecessor is the right most node of the left subtree
Else we walk up the ancestor chain until you traverse the first right child pointer (find the first node that is a right child of its
parent...that parent is the predecessor)
If you get to the root w/o finding a node that is a right child, there is no predecessor
*/
template<class Key, class Value> std::pair<const typename tree234<Key, Value>::Node *, int> tree234<Key, Value>::iterator::getLeafNodePredecessor(const Node *pnode, int index)
{
// Handle trivial case: if the leaf node is not a 2-node (it is a 3-node or 4-node, and key_index is not the first key), simply set index of predecessor to index - 1.
if (!pnode->isTwoNode() && index != 0) {
return {pnode, index - 1};
}
// Get child_index such that pnode == pnode->parent->children[child_index]
auto child_index = pop();
if (child_index != 0) { // If pnode is not the left-most child, the predecessor is in the parent
return {pnode->parent, child_index - 1};
} else {
/*
To find the next smallest node the logic is similar to finding the successor: We walk up the parent chain until we traverse the first parent that
is not a left-most child of its parent. That parent is the predecessor. If we get to the root without finding a node that is a right child, there is no predecessor.
Note: In a 2 3 tree, a "right" child pointer will be either the second child of a 2-node or the second, the middle, or the third child of a 3-node. "right" child
pointer means a pointer to a subtree with larger keys. In a 2 3 tree, the middle child pointer of a 3-node parent is a "right child pointer" of the 1st key
because all the keys of the subtree whose root is the second (or middle) child pointer are greater than 1st key of the subtree's parent.
So when we walk up the ancestor chain as long as the parent is the first child. For example, in the tree portion shown below
[5, 10]
/ | \
... ... [27, 70]
/ | \
/ | \
[20] [45] [80, 170]
/ \ / \ / | \
[15] [25] [30] [60] <-- pnode points to leaf node [20].
/ \ / \ / \ / \
0 0 0 0 0 0 0 0 ...
if [15] is the pnode leaf node, the predecessor of [15] is the second key of the 3-node [5, 10] because when we walk up the parent chain from [15], the first
right child pointer we encounter is the parent of [27, 70], which is [5, 10]. So [10] is the next smallest key. In this example
[5, 10]
/ | \
... ... [27, 70]
/ | \
/ | \
[20] [45] [80, 170]
/ \ / \ / | \
[15] [25] [30] [60] <-- pnode points to leaf node [20].
/ \ / \ / \ / \
0 0 0 0 0 0 0 0 ...
if [30] is the pnode leaf node, the predecessor of [30] is the first key of the 3-node [27, 70] because when we walk up the parent chain from [30], the first
non-first child pointer we encounter is the parent of [45], which is [27, 70]. So the key at index 0, which is [27], is the next smallest key. Therefore, if our
loop above terminates without encountering the root, we must determine the child index of prior_node in pnode. If pnode is a 2-node, it is trivial: the child
index is one. If pnode is a three node, the child index is either one or two:
int child_index = 1; // assume pnode is a 2-node.
if (pnode->isThreeNode()) { // if it is a 3-nodee, compare prior_node to children[1]
child_index = prior_node == pnode->children[1].get() ? 1 : 2;
}
Now that we know the child_index such that
pnode->children[child_index] == prior_node;
Determine which key is the predecessor. If child_index is one, the middle child, then the predecessor is pnode->keys_values[0]. If child_index is two, then
the predecessor is pnode->key(1). Thus, the predecessor is the key at child_index - 1.
*/
const Node *parent = pnode->parent;
// Ascend upward the parent pointer as long as the child continues to be the left most child (of its parent).
for(;child_index == 0; parent = pnode->parent) {
// child is still the left most child, but if it is also the root, then, there is no predecessor. child holds the smallest key in the tree.
if (parent == tree.root.get()) {
return {nullptr, 0}; // {nullptr, 0} indicates "no predecessor".
}
child_index = pop();
pnode = parent;
}
// The predecessor will be the first key, starting with the right most key, that is less than current_key.
return {parent, child_index - 1};
} // end else
}
// copy assignment
template<typename Key, typename Value> inline tree234<Key, Value>& tree234<Key, Value>::operator=(const tree234& lhs) noexcept
{
if (this == &lhs) {
return *this;
}
destroy_subtree(root); // free all the nodes of the current tree
tree_size = lhs.tree_size;
copy_tree(lhs.root, root);
return *this;
}
template<typename Key, typename Value> inline void tree234<Key, Value>::Node::printKeys(std::ostream& ostr)
{
ostr << "[";
for(auto i = 0; i < getTotalItems(); ++i) {
ostr << keys_values[i].__get_value().first;
if (i < get_lastkey_index()) { //getTotalItems() - 1) {
ostr << ", ";
}
}
ostr << "]";
}
template<typename Key, typename Value> inline constexpr int tree234<Key, Value>::Node::getTotalItems() const noexcept
{
return totalItems;
}
template<typename Key, typename Value> inline constexpr int tree234<Key, Value>::Node::getChildCount() const noexcept
{
return totalItems + 1;
}
template<typename Key, typename Value> inline constexpr bool tree234<Key, Value>::Node::isTwoNode() const noexcept
{
return (totalItems == static_cast<int>(NodeType::two_node)) ? true : false;
}
template<typename Key, typename Value> inline constexpr bool tree234<Key, Value>::Node::isThreeNode() const noexcept
{
return (totalItems == static_cast<int>(NodeType::three_node)) ? true : false;
}
template<typename Key, typename Value> inline constexpr bool tree234<Key, Value>::Node::isFourNode() const noexcept
{
return (totalItems == static_cast<int>(NodeType::four_node)) ? true : false;
}
template<typename Key, typename Value> inline constexpr bool tree234<Key, Value>::Node::isEmpty() const noexcept
{
return (totalItems == 0) ? true : false;
}
template<typename Key, typename Value> inline constexpr int tree234<Key, Value>::size() const
{
return tree_size;
}
template<typename Key, typename Value> inline int tree234<Key, Value>::height() const noexcept
{
int depth = 0;
for (auto current = root.get(); current; current = current->children[0].get()) {
++depth;
}
return depth;
}
// Move assignment operator
template<typename Key, typename Value> inline tree234<Key, Value>& tree234<Key, Value>::operator=(tree234&& lhs) noexcept
{
tree_size = lhs.tree_size;
lhs.tree_size = 0;
root = std::move(lhs.root);
root->parent = nullptr;
}
/*
* F is a functor whose function call operator takes a 1.) const Node * and an 2.) int, indicating the depth of the node from the root,
* which has depth 1.
*/
template<typename Key, typename Value> template<typename Functor> void tree234<Key, Value>::levelOrderTraverse(Functor f) const noexcept
{
if (!root.get()) return;
// pair of: 1. const Node * and 2. level of tree.
std::queue<std::pair<const Node*, int>> queue;
auto level = 1;
queue.push({root.get(), level});
while (!queue.empty()) {
auto& [pnode, tree_level] = queue.front();
f(pnode, tree_level); // Call functor
if (!pnode->isLeaf()) { // If it was not a leaf node, push its children onto the queue
for(auto i = 0; i < pnode->getChildCount(); ++i) {
queue.push({pnode->children[i].get(), tree_level + 1});
}
}
queue.pop(); // Remove the node used in the call to functor f above.
}
}
/*
* This method allows the tree to be traversed in-order step-by-step
*/
template<typename Key, typename Value> template<typename Functor> inline void tree234<Key, Value>::iterativeInOrderTraverse(Functor f) const noexcept
{
const Node *current = min(root.get());
int key_index = 0;
while (current) {
f(current->pair(key_index));
//std::pair<const Node *, int> pair = getSuccessor(current, key_index);
auto &&[next_pnode, next_index] = getSuccessor(current, key_index);
current = next_pnode;
key_index = next_index;
}
}
/*
* Return the node with the "smallest" key in the tree, the left most left node.
*/
template<typename Key, typename Value> inline const typename tree234<Key, Value>::Node *tree234<Key, Value>::min(const Node *current) const noexcept
{
while (current->children[0])
current = current->children[0].get();
return current;
}
/*
* Return the node with the largest key in the tree, the right most left node.
*/
template<typename Key, typename Value> inline const typename tree234<Key, Value>::Node *tree234<Key, Value>::max(const Node *current) const noexcept
{
while (current->getRightMostChild())
current = current->getRightMostChild();
return current;
}
template<typename Key, typename Value> template<typename Functor> inline void tree234<Key, Value>::inOrderTraverse(Functor f) const noexcept
{
DoInOrderTraverse(f, root.get());
}
template<typename Key, typename Value> template<typename Functor> inline void tree234<Key, Value>::postOrderTraverse(Functor f) const noexcept
{
DoPostOrderTraverse(f, root);
}
template<typename Key, typename Value> template<typename Functor> inline void tree234<Key, Value>::preOrderTraverse(Functor f) const noexcept
{
DoPreOrderTraverse(f, root.get());
}
template<typename Key, typename Value> template<typename Functor> inline void tree234<Key, Value>::debug_dump(Functor f) noexcept
{
DoPostOrder4Debug(f, root.get());
}
/*
* Calls functor on each node in post order. Uses recursion.
*/
template<typename Key, typename Value> void tree234<Key, Value>::destroy_subtree(std::unique_ptr<Node>& current) noexcept
{
if (!current) return;
switch (current->getTotalItems()) {
case 1: // two node
destroy_subtree(current->children[0]);
destroy_subtree(current->children[1]);
current.reset();
break;
case 2: // three node
destroy_subtree(current->children[0]);
destroy_subtree(current->children[1]);
destroy_subtree(current->children[2]);
current.reset();
break;
case 3: // four node
destroy_subtree(current->children[0]);
destroy_subtree(current->children[1]);
destroy_subtree(current->children[2]);
destroy_subtree(current->children[3]);
current.reset();
break;
}
}
/*
* Calls functor on each node in post order. Uses recursion.
*/
template<typename Key, typename Value> template<typename Functor> void tree234<Key, Value>::DoPostOrderTraverse(Functor f, const Node *current) const noexcept
{
if (!current) return;
switch (current->getTotalItems()) {
case 1: // two node
DoPostOrderTraverse(f, current->children[0].get());
DoPostOrderTraverse(f, current->children[1].get());
f(current->get_value(0));
break;
case 2: // three node
DoPostOrderTraverse(f, current->children[0].get());
DoPostOrderTraverse(f, current->children[1].get());
f(current->get_value(0));
DoPostOrderTraverse(f, current->children[2].get());
f(current->get_value(1));
break;
case 3: // four node
DoPostOrderTraverse(f, current->children[0].get());
DoPostOrderTraverse(f, current->children[1].get());
f(current->get_value(0));
DoPostOrderTraverse(f, current->children[2].get());
f(current->get_value(1));
DoPostOrderTraverse(f, current->children[3].get());
f(current->get_value(1));
break;
}
}
/*
* Calls functor on each node in pre order. Uses recursion.
*/
template<typename Key, typename Value> template<typename Functor> void tree234<Key, Value>::DoPreOrderTraverse(Functor f, const Node *current) const noexcept
{
if (!current) return;
f(current->get_value(0)); // Visit keys_values[0]
switch (current->getTotalItems()) {
case 1: // two node
DoPreOrderTraverse(f, current->children[0].get());
DoPreOrderTraverse(f, current->children[1].get());
break;
case 2: // three node
DoPreOrderTraverse(f, current->children[0].get());
DoPreOrderTraverse(f, current->children[1].get());
f(current->get_value(1));// Visit Node::keys_values[1]
DoPreOrderTraverse(f, current->children[2].get());
break;
case 3: // four node
DoPreOrderTraverse(f, current->children[0].get());
DoPreOrderTraverse(f, current->children[1].get());
f(current->get_value(1));// Visit Node::keys_values[1]
DoPreOrderTraverse(f, current->children[2].get());
f(current->get_value(2));// Visit Node::keys_values[2]
DoPreOrderTraverse(f, current->children[3].get());
break;
}
}
/*
* Calls functor on each node in in-order traversal. Uses recursion.
*/
template<typename Key, typename Value> template<typename Functor> void tree234<Key, Value>::DoInOrderTraverse(Functor f, const Node *current) const noexcept
{
if (!current) return;
switch (current->getTotalItems()) {
case 1: // two node
DoInOrderTraverse(f, current->children[0].get());
f(current->get_value(0));
DoInOrderTraverse(f, current->children[1].get());
break;
case 2: // three node
DoInOrderTraverse(f, current->children[0].get());
f(current->get_value(0));
DoInOrderTraverse(f, current->children[1].get());
f(current->get_value(1));
DoInOrderTraverse(f, current->children[2].get());
break;
case 3: // four node
DoInOrderTraverse(f, current->children[0].get());
f(current->get_value(0));
DoInOrderTraverse(f, current->children[1].get());
f(current->get_value(1));
DoInOrderTraverse(f, current->children[2].get());
f(current->get_value(2));
DoInOrderTraverse(f, current->children[3].get());
break;
}
}
/*
* Preconditionss: childIndex is within the range for the type of node, and child is not nullptr.
*
* connectChild() adopts input child node as its (childIndex + 1)th child by doing:
*
* children[childIndex] = std::move(child);
* children[childIndex]->parent = this;
*
*/
template<typename Key, typename Value> inline void tree234<Key, Value>::Node::connectChild(int childIndex, std::unique_ptr<Node>& child) noexcept
{
children[childIndex] = std::move( child );
if (children[childIndex]) {
children[childIndex]->parent = this;
}
}
/*
* Require: childIndex is within the range for the type of node.
* Returns: child pointer.
* Note: disconnectChild() must always be called before removeItem(); otherwise, it will not work correctly (because totalItems
* will have been altered).
*/
template<typename Key, typename Value> inline std::unique_ptr<typename tree234<Key, Value>::Node> tree234<Key, Value>::Node::disconnectChild(int childIndex) noexcept // ok
{
std::unique_ptr<Node> node{ std::move(children[childIndex] ) }; // invokes unique_ptr<Node> move ctor.
// shift children (whose last 0-based index is totalItems) left to overwrite removed child i.
for(auto i = childIndex; i < getTotalItems(); ++i) {
children[i] = std::move(children[i + 1]); // shift remaining children to the left.
}
return node;
}
/*
* Returns tuple of three values: <bool, Node *, int>.
* If key found n this Node, we return this tuple: {true, pointer to node containing key, the index into Node::key_values of the key}.
* If key is not found, we return this tuple: {false, pointer to next child with which to continue the downward search of the tree, 0}.
*/
template<class Key, class Value> inline std::tuple<bool, typename tree234<Key, Value>::Node *, int> tree234<Key, Value>::Node::find(Key lhs_key) const noexcept
{
for(auto i = 0; i < getTotalItems(); ++i) {
if (lhs_key < key(i)) {
return {false, children[i].get(), 0};
} else if (key(i) == lhs_key) {
return {true, const_cast<Node *>(this), i};
}
}
// lhs_key must be greater than the last key (because it is not less than or equal to it).
// next = children[totalItems].get();
return {false, children[getTotalItems()].get(), 0};
}
/*
* Input: Assumes that "this" is never the root (because the parent of the root is always the nullptr).
*/
template<class Key, class Value> int tree234<Key, Value>::Node::getChildIndex() const noexcept
{
// Determine child_index such that this == this->parent->children[child_index]
int child_index = 0;
for (; child_index <= parent->getTotalItems(); ++child_index) {
if (this == parent->children[child_index].get())
break;
}
return child_index;
}
template<typename Key, typename Value> inline constexpr bool tree234<Key, Value>::Node::isLeaf() const noexcept // ok
{
return !children[0] ? true : false;
}
/*
* Recursive version of find
*/
template<typename Key, typename Value> inline bool tree234<Key, Value>::find(Key key) const noexcept
{
return find(root.get(), key);
}
/*
* Recursive main find method. Return true if found, false otherwise.
*/
template<typename Key, typename Value> bool tree234<Key, Value>::find(const Node *pnode, Key key) const noexcept
{
if (!pnode) return false;
auto i = 0;
for (;i < pnode->getTotalItems(); ++i) {
if (key < pnode->key(i))
return find(pnode->children[i].get(), key);
else if (key == pnode->key(i))
return true;
}
return find(pnode->children[i].get(), key);
}
/*
* Preconditions: node is not a four node, and key is not present in node.
* Purpose: Shifts keys_values needed so key can be inserted in sorted position. Returns index of inserted key.
*/
template<typename Key, typename Value> int tree234<Key, Value>::Node::insert(const Key& lhs_key, const Value& lhs_value) noexcept // ok. Maybe add a move version, too: insertKey(Key, Value&&)
{
// start on right, examine items
for(auto i = get_lastkey_index(); i >= 0 ; --i) {
if (lhs_key < key(i)) { // if key[i] is bigger
keys_values[i + 1] = std::move(keys_values[i]); // shift it right
} else {
keys_values[i + 1].__ref() = std::make_pair<const key_type&, const mapped_type&>(lhs_key, lhs_value);
++totalItems; // increase the total item count
return i + 1; // return index of inserted key.
}
}
// key is smaller than all keys_values, so insert it at position 0
keys_values[0].__ref() = std::make_pair<const key_type&, const mapped_type&>(lhs_key, lhs_value);
++totalItems; // increase the total item count
return 0;
}
/*
* Inserts key_value pair into its sorted position in this Node and makes largerNode its right most child.
*/
template<typename Key, typename Value> void tree234<Key, Value>::Node::insert(__value_type<Key, Value>&& vt_in, std::unique_ptr<Node>& largerNode) noexcept
{
// start on right, examine items
for(auto i = get_lastkey_index(); i >= 0 ; --i) {
if (vt_in.__ref().first < key(i)) { // if key[i] is bigger
keys_values[i + 1] = std::move(keys_values[i]); // shift it right...
} else {
keys_values[i + 1] = std::move(vt_in);
++totalItems; // increase the total item count
insertChild(i + 2, largerNode);
return; // return index of inserted key.
}
}
// key is smaller than all keys_values, so insert it at position 0
keys_values[0] = std::move(vt_in);
++totalItems; // increase the total item count
insertChild(1, largerNode);
return;
}
/*
Input: A new child to insert at child index position insert_index. The current number of children currently is given by children_num.
*/
template<typename Key, typename Value> void tree234<Key, Value>::Node::insertChild(int insert_index, std::unique_ptr<Node>& newChild) noexcept
{
// While Node::totalItems reflects the correct number of keys, the number of children currently is also equal to the number of keys.
// ...move its children right, starting from its last child index and stopping just before insert_index.
for(auto i = get_lastkey_index(); i >= insert_index; i--) {
connectChild(i + 1, children[i]);
}
// Then insert the new child whose key is larger than key_value.key().
connectChild(insert_index, newChild);
}
/*
* Insert and Delete algorithms are based on these link
*
* https://www.cs.ubc.ca/~liorma/cpsc320/files/B-trees.pdf
* https://www.cs.purdue.edu/homes/ayg/CS251/slides/chap13a.pdf
* https://www.cs.mcgill.ca/~cs251/ClosestPair/2-4trees.html
* https://algorithmtutor.com/Data-Structures/Tree/2-3-4-Trees/
*
* We reduce deletion of an internal node's key to deletion of a leaf node's key by swapping the key to be deleted
* with its in-order successor and then deleting the key from the leaf. To prevent deletion from a 2-node leaf, which
* would leave an empty node (underflow), we convert all 2-nodes as we descend the tree to 3- or 4-nodes using the stratagies below.
*
* If the key is an internal node, then its successor will be the minimum key of its first right subtree. To ensure that the successor of the
* internal node is not a 2-node, we again convert all 2-nodes to 3- or 4-nodes as we descend. If the right subtree root is itself a 2-node, when it
* is converted, the key to be delete may move down into it (as its first or second key), so we check for this.
*
* Conversion of 2-node has two cases:
* Case 1: If an adjacent sibling has is a 3- or 4-node, we "steal" a sibling key by rotating it into the parent and bringing down a parent key into the 2-node,
*
* Case 2: If each adjacent sibling (there are at most two) is a 2-node, we canvert the 2-node into a 4-node by merging into it a sibling key and a key from parent (which we
* know is not a 2-node). The children affected are shifted and adopted(see code).
*
* Special case: If the root holds the key to be deleted, we meris a 2-node
*/
template<class Key, class Value> bool tree234<Key, Value>::remove(Key key)
{
if (!root) return false;
else if (root->isLeaf()) {
int index = 0;
for (; index < root->getTotalItems(); ++index) {
if (root->key(index) == key) {
// Remove key from root and puts its in-order successor (if it exists) into its place.
root->removeKeyValue(index);
if (root->isEmpty()) {
root.reset();
}
--tree_size;
return true;
}
}
return false;
} else { // there are more nodes than just the root.
auto rc = remove(root.get(), key);
if (rc) --tree_size;
return rc;
}
}
template<typename Key, typename Value> inline __value_type<Key, Value> tree234<Key, Value>::Node::removeKeyValue(int index) noexcept
{
__value_type<Key, Value> key_value = std::move(keys_values[index]); // Return value
// shift to the left all keys_values to the right of index to the left
for(auto i = index; i < get_lastkey_index(); ++i) {
keys_values[i] = std::move(keys_values[i + 1]);
}
--totalItems;
return key_value;
}
/*
* Input: right subtree from which to remove key.
* Return: true if key removed. false if key not found.
*/
template<class Key, class Value> bool tree234<Key, Value>::remove(Node *psubtree, Key key)
{
auto [found, pdelete, delete_index] = find_delete_node(psubtree, key);
if (!found) return false;
if (pdelete->isLeaf()) {
// Remove from leaf node
pdelete->removeKeyValue(delete_index);
} else { // Internal node. Find successor, converting 2-nodes as we search and resetting pdelete and delete_index if necessary.
// find min and convert 2-nodes as we search.
auto[pdelete_, delete_index_, psuccessor] = get_delete_successor(pdelete, key, delete_index);
pdelete_->keys_values[delete_index_] = std::move(psuccessor->keys_values[0]); // simply overwrite key to be deleted with its successor.
psuccessor->removeKeyValue(0); // Since successor is not in a 2-node, we can delete it from the leaf.
}
return true;
}
/*
Input: Node * and its child index in parent
Return: {bool: found/not found, Node *pFound, int key_index within pFound}
*/
template<class Key, class Value> std::tuple<bool, typename tree234<Key, Value>::Node *, int> tree234<Key, Value>::find_delete_node(Node *pcurrent, Key delete_key, int child_index) noexcept
{
if (nullptr == pcurrent)
return {false, pcurrent, 0};
if (pcurrent->isTwoNode()) {
// Special case: root is a 2-node with two 2-node children.
if (pcurrent == root.get() && root->children[0]->isTwoNode() && root->children[1]->isTwoNode())
pcurrent->make4Node();
else if (pcurrent != root.get())
convert2Node(pcurrent, child_index);
}
// Search for it, and if found, return it.
auto i = 0;
for(;i < pcurrent->getTotalItems(); ++i) {
if (delete_key == pcurrent->key(i))
// Found delete_key to be deleted is at pcurrent->key(i).
return {true, pcurrent, i};
if (delete_key < pcurrent->key(i))
// Recurse with left child of pcurrent.
return find_delete_node(pcurrent->children[i].get(), delete_key, i);
}
// If not found and delete_key is larger than all keys, recurse with right most child
return find_delete_node(pcurrent->children[i].get(), delete_key, i);
}
/*
* Input: pdelete->key(delete_key_index) is key to be deleted.
*
* Locates the in-order successor node and converts 2-nodes encountered into 3- or 4-nodes to ensure that the in-order successor key/value can be removed
* without leaving an empty node.
*
* Returns tuple with location of delete node and key to be delete (as it may have moved) and the delete successor node (which will be a leaf node)
* Returns these are a 3-element tuple:
* - pointer to node with key to be deleted (as it may have moved in the tree).
* - along with the index of key to be deleted,
* - pointer to successor.
*/
template<class Key, class Value> std::tuple<typename tree234<Key, Value>::Node *, int, typename tree234<Key, Value>::Node *>
tree234<Key, Value>::get_delete_successor(Node *pdelete, Key delete_key, int delete_key_index) noexcept
{
// Get pointer to right subtree.
auto child_index = delete_key_index + 1;
Node *rightSubtree = pdelete->children[child_index].get();
// If it's a 2-node, convert it to a 3- or 4-node.
if (rightSubtree->isTwoNode()) {
// Set child_index: parent->children[child_index] == 'the converted 2-node'.
child_index = convert2Node(rightSubtree, child_index);
/*
Check if delete_key moved...
Comments: If the root of the right subtree had to be converted, then either a rotation occurred, or a fusion (with the parent, rightSubtree and a
sibling occurred). If a fusion of the rightSubtree with a parent key and a sibling key occurred, delete_key becomes the 2nd key in rightSubtree.
If a left rotation occurred (that "stole" a key from the left sibling and brought down the delete_key), then delete_key
becomes the first key of rightSubtree. If a right rotation occurred, delete_key is unaffected. This applies regardless whether pdelete is a 3-node
or a 4-node.
Thus: If a fusion of the rightSubtree with a parent key and a sibling key occurred, delete_key becomes the 2nd key in rightSubtree. If a left rotation occurred,
delete_key becomes the first key of rightSubtree.
*/
if (delete_key == rightSubtree->key(0) || delete_key == rightSubtree->key(1)) {
// ...reset delete_key_index, and...
delete_key_index = (delete_key == rightSubtree->key(0)) ? 0 : 1;
if (rightSubtree->isLeaf()) { // ...if rightSubtree is a leaf, we're done; otherwise, we...
return {rightSubtree, delete_key_index, rightSubtree};
}
// ... recurse, passing the just-converted rightSubtree and the new delete_key_index value.
return get_delete_successor(rightSubtree, delete_key, delete_key_index);
}
}
// We only get here if rightSubtree was not a leaf.
// Finds the left-most node of the right subtree and converts all 2-nodes encountered.
Node *psuccessor = get_successor_node(rightSubtree, child_index);
return {pdelete, delete_key_index, psuccessor};
}
template<typename Key, typename Value> inline constexpr const typename tree234<Key, Value>::Node *tree234<Key, Value>::Node::getParent() const noexcept // ok
{
return parent;
}
/*
* Requires: pnode is 2-node.
* Returns: pnode is converted into either a 3- or a 4-node and .
*
* Code follows pages 51-53 of: www.serc.iisc.ernet.in/~viren/Courses/2009/SE286/2-3Trees-Mod.ppt
* and pages 64-66 of http://www2.thu.edu.tw/~emtools/Adv.%20Data%20Structure/2-3,2-3-4%26red-blackTree_952.pdf
*
* Case 1: If an adjacent sibling--there are at most two--has 2 or 3 items, "steal" an item from the sibling by
* rotating items and shifting children. See slide 51 of www.serc.iisc.ernet.in/~viren/Courses/2009/SE286/2-3Trees-Mod.ppt
*
* Case 2: If each adjacent sibling has only one item (and parent is a 3- or 4-node), we take its sole item together with an item from
* parent and fuse them into the 2-node, making a 4-node. If the parent is also a 2-node (this only happens in the case of the root),
* we fuse the three together into a 4-node. In either case, we shift the children as required.
*
*/
template<typename Key, typename Value> int tree234<Key, Value>::convert2Node(Node *pnode, int child_index) noexcept
{
// Determine if any adjacent sibling has a 3- or 4-node, preferring the right adjacent sibling.
auto [has3or4NodeSibling, sibling_index] = pnode->chooseSibling(child_index);
return has3or4NodeSibling ? make3Node(pnode, child_index, sibling_index) : make4Node(pnode->getParent(), child_index, sibling_index);
}
/*
* Returns: pair<bool, int>
* first -- if first true is there is a 3 or 4 node sibling; otherwise, false implies all siblings are 2-nodes
* second -- contains the child index of the sibling to be used.
*
*/
template<typename Key, typename Value> inline std::pair<bool, int> tree234<Key, Value>::Node::chooseSibling(int child_index) const noexcept
{
int left_adjacent = child_index - 1;
int right_adjacent = child_index + 1;
bool has3or4NodeSibling = false;
int parentChildrenTotal = parent->getChildCount();
int sibling_index = left_adjacent; // We assume sibling is to the left unless we discover otherwise.
if (right_adjacent < parentChildrenTotal && !parent->children[right_adjacent]->isTwoNode()) {
has3or4NodeSibling = true;
sibling_index = right_adjacent;
} else if (left_adjacent >= 0 && !parent->children[left_adjacent]->isTwoNode()) {
has3or4NodeSibling = true;
sibling_index = left_adjacent;
} else if (right_adjacent < parentChildrenTotal) { // There are no 3- or 4-nodes siblings. Therefore the all siblings
// are 2-node(s).
sibling_index = right_adjacent;
}
return {has3or4NodeSibling, sibling_index};
}
/*
* Requirements:
* 1. Parent node is a 2-node, and its two children are also both 2-nodes. Parent must be the tree's root (this is an inherent property of the
* 2 3 4 tree insertion algorithm).
*
* Promises:
* 1. 4-node resulting from fusing of the two 2-nodes' keys_values into the parent.
* 2. Adoption of the 2-node children's children as children of parent.
*
* Pseudo code:
*
* 1. Absorbs its children's keys_values as its own.
* 2. Makes its grandchildren its children.
*/
template<typename Key, typename Value> typename tree234<Key, Value>::Node *tree234<Key, Value>::Node::make4Node() noexcept
{
// move key of 2-node
keys_values[1] = std::move(keys_values[0]);
// absorb children's keys_values
keys_values[0] = std::move(children[0]->keys_values[0]);
keys_values[2] = std::move(children[1]->keys_values[0]);
totalItems = 3;
std::unique_ptr<Node> leftOrphan {std::move(children[0])}; // These two Nodes will be freed upon return.
std::unique_ptr<Node> rightOrphan {std::move(children[1])};
connectChild(0, leftOrphan->children[0]);
connectChild(1, leftOrphan->children[1]);
connectChild(2, rightOrphan->children[0]);
connectChild(3, rightOrphan->children[1]);
return this;
}
/*
* Input:
* Node to convert
* Its sibling index
* Its child index in parent
*
* returns:
* p2node is now a three node
* child_index, which is not changed at all.
*
*/
template<typename Key, typename Value> int tree234<Key, Value>::make3Node(Node *p2node, int child_index, int sibling_index) noexcept
{
auto parent = p2node->getParent();
Node *psibling = parent->children[sibling_index].get();
// First we get the index of the parent's key value such that either
//
// parent->children[child_index]->keys_values[0] < parent->keys_values[index] < parent->children[sibling_id]->keys_values[0]
//
// or
//
// parent->children[sibling_id]->keys_values[0] < parent->keys_values[index] < parent->children[child_index]->keys_values[0]
//
// by taking the minimum of the indecies.
int parent_key_index = std::min(child_index, sibling_index);
/* If sibling is to the left, then this relation holds
*
* parent->children[sibling_id]->keys_values[0] < parent->keys_values[index] < parent->children[child_index]->keys_values[0]
*
* and we do a right rotation
*
* else sibling is to the right and this relation holds
*
* parent->children[child_index]->keys_values[0] < parent->keys_values[index] < parent->children[sibling_id]->keys_values[0]
*
* therefore we do a left rotation
*/
(child_index > sibling_index) ? rightRotation(p2node, psibling, parent, parent_key_index) : leftRotation(p2node, psibling, parent, parent_key_index);
return child_index;
}
/*
* Requires: sibling is to the left, therefore: parent->children[sibling_id]->keys_values[0] < parent->keys_values[index] < parent->children[node2_index]->keys_values[0]
*/
template<typename Key, typename Value> typename tree234<Key, Value>::Node *tree234<Key, Value>::rightRotation(Node *p2node, Node *psibling, Node *parent, int parent_key_index) noexcept
{
// Add the parent's key to 2-node, making it a 3-node
// 1. But first shift the 2-node's sole key right one position
p2node->keys_values[1] = p2node->keys_values[0];
p2node->keys_values[0] = parent->keys_values[parent_key_index]; // 2. Now bring down parent key
p2node->totalItems = static_cast<int>(tree234<Key, Value>::Node::NodeType::three_node); // 3. increase total items
int total_sibling_keys_values = psibling->getTotalItems();
// Disconnect right-most child of sibling
std::unique_ptr<Node> pchild_of_sibling = psibling->disconnectChild(total_sibling_keys_values);
// remove the largest, the right-most, sibling's key, and, then, overwrite parent item with largest sibling key
parent->keys_values[parent_key_index] = std::move(psibling->removeKeyValue(total_sibling_keys_values - 1));
p2node->insertChild(0, pchild_of_sibling); // add former right-most child of sibling as its first child
return p2node;
}
/* Requires: sibling is to the right therefore: parent->children[node2_index]->keys_values[0] < parent->keys_values[index] < parent->children[sibling_id]->keys_values[0]
* Do a left rotation
*/
template<typename Key, typename Value> typename tree234<Key, Value>::Node *tree234<Key, Value>::leftRotation(Node *p2node, Node *psibling, Node *parent, int parent_key_index) noexcept
{
// pnode2->keys_values[0] doesn't change.
p2node->keys_values[1] = parent->keys_values[parent_key_index]; // 1. insert parent key making 2-node a 3-node
p2node->totalItems = static_cast<int>(tree234<Key, Value>::Node::NodeType::three_node);// 3. increase total items
std::unique_ptr<Node> pchild_of_sibling = psibling->disconnectChild(0); // disconnect first child of sibling.
// Remove smallest key in sibling
parent->keys_values[parent_key_index] = std::move(psibling->removeKeyValue(0));
// add former first child of silbing as right-most child of our 3-node.
p2node->insertChild(p2node->getTotalItems(), pchild_of_sibling);
return p2node;
}
/*
* Requirements:
* 1. parent->children[node2_index] and parent->children[sibling_index] are both 2-nodes
* 2. parent is a 3- or 4-node. We know this since the special case of a root 2-node with two 2-node cildren was already handled, so even if the root is the parent
* it will not be a 2-node.
*
* Promises:
*
* 1. The 2-node at parent->children[node2_index] is converted into a 4-node by fusing it with the 2-node at parent->children[sibling_index] along with
* a key from the parent located at parent->keys_values[parent_key_index]
*
* 2. The 2-node sibling at parent->children[silbing_index] is deleted from the tree, and its children are connected to the converted 2-node (into a 4-node)
*
* 3. parent->childen[node2_id] is the 2-node being converted (into a 3- or 4-node) <--Incorrect!
*
* 4. The parent becomes either a 2-node, if it was a 3-node, or a 2-node if it was a 4-node?
*
* Returns: child_index such that parent->children[child_index] == 'the converted 2-node'.
*/
template<typename Key, typename Value> int tree234<Key, Value>::make4Node(Node *parent, int node2_index, int sibling_index) noexcept
{
Node *p2node = parent->children[node2_index].get();
auto child_index = node2_index;
// First get the index of the parent's key value to be stolen and added into the 2-node
if (int parent_key_index = std::min(node2_index, sibling_index); node2_index > sibling_index) { // sibling is to the left.
// Since sibling if to the left, p2node will become the child one position to the left of where it was, ie, one less than its current value.
--child_index;
/* Adjust parent:
1. Remove parent key (and shift its remaining keys_values and reduce its totalItems)
2. Reset parent's children pointers after removing sibling.
* Note: There is a potential insidious bug: disconnectChild depends on totalItems, which removeKey() reduces. Therefore,
* disconnectChild() must always be called before removeKey().
*/
std::unique_ptr<Node> psibling = parent->disconnectChild(sibling_index); // This will do #2.
__value_type<Key, Value> parent_key_value = parent->removeKeyValue(parent_key_index); //this will do #1
// Now, add both the sibling's and parent's key to 2-node
// 1. But first shift the 2-node's sole key right two positions
p2node->keys_values[2] = p2node->keys_values[0];
p2node->keys_values[1] = std::move(parent_key_value); // 2. bring down parent key and value, ie, its pair<Key, Value>, so a move assignment operator must be invoked.
p2node->keys_values[0] = psibling->keys_values[0]; // 3. insert adjacent sibling's sole key.
p2node->totalItems = 3; // 3. increase total items
// Add sibling's children to the former 2-node, now 4-node...
p2node->children[3] = std::move(p2node->children[1]); // ... but first shift its children right two positions
p2node->children[2] = std::move(p2node->children[0]);
// Insert sibling's first two child. Note: connectChild() will also reset the parent pointer of these children (to be p2node).
p2node->connectChild(1, psibling->children[1]);
p2node->connectChild(0, psibling->children[0]);
// <-- automatic deletion of psibling in above after } immediately below
} else { // sibling is to the right of p2node
//Node: child_index will not be affected if the sibling is to the righ
/* Next adjust parent:
* 1. Remove parent key (and shift its remaining keys_values and reduce its totalItems)
* 2. Reset its children pointers
*
* Note: disconnectChild() must always be called before removeKey() because disconnectChild() depends on totalItems, which removeKey() alters; otherwise, the children
* will not be shifted correctly.There is a potential insidious bug: disconnectChild depends on totalItems, which removeKey reduces.
*/
std::unique_ptr<Node> psibling = parent->disconnectChild(sibling_index); // this does #2
p2node->keys_values[1] = parent->removeKeyValue(parent_key_index); // this will #1 // 1. bring down parent key
p2node->keys_values[2] = std::move(psibling->keys_values[0]);// 2. insert sibling's sole key and value.
p2node->totalItems = 3; // 3. make it a 4-node
// Insert sibling's last two child. Note: connectChild() will also reset the parent pointer of these children (to be p2node).
p2node->connectChild(3, psibling->children[1]); // Add sibling's children
p2node->connectChild(2, psibling->children[0]);
} // <-- automatic deletion of psibling's underlying raw memory
return child_index;
}
/*
* Insersion algorithm is based on https://www.cs.ubc.ca/~liorma/cpsc320/files/B-trees.pdf
*
* Other helpful links are:
*
* https://www.cs.usfca.edu/~galles/visualization/BTree.html <-- Best manually insert/delete animation
* https://www.educative.io/page/5689413791121408/80001 <-- Top notch animation of insert and delete.
* https://www.cs.purdue.edu/homes/ayg/CS251/slides/chap13a.pdf <-- Has good illustrations
* https://www.cs.mcgill.ca/~cs251/ClosestPair/2-4trees.html
* https://algorithmtutor.com/Data-Structures/Tree/2-3-4-Trees/ <-- Introduces reb-black trees, too
*
* Insertion Algorithm
*
* The insert algorithm is based on the this description of `B-Trees <https://www.cs.ubc.ca/~liorma/cpsc320/files/B-trees.pdf>`_. New keys are inserted at leaf nodes.
* If the leaf node is a 4-node, we must first split it by pushing its middle key up a level to make room for the new key. To ensure the parent can always accomodate a
* key, we must first split the parent if it is a 4-node. And to ensure the parent's parent can accomodate a new key, we split all 4-nodes as we descend the tree.
*
* If the root must be split (because it is the parent of the leaf or is itself a leaf), the tree will grows upward when a new root node is inserted above the old.
*
* The split algorithm converts the fromer 4-node into 2-node that containing only its left key. This downsized node retains it two left-most children. The middle key is
* pushed into the parent, and the right key is moved into a new 2-node. This newly created 2-node takes ownership of the two right-most children of the former 4-node, and
* this newly created 2-node is made a child of the parent. The child indexes in the parent are adjusted to properly reflect the new relationships between these nodes.
*
*/
template<typename Key, typename Value> void tree234<Key, Value>::insert(const Key& new_key, const Value& value) noexcept
{
if (!root) {
root = std::make_unique<Node>(new_key, value);
++tree_size;
return;
}
auto [bool_found, current, index] = find_insert_node(root.get(), new_key);
if (bool_found) return;
// current node is now a leaf and it is not full (because we split all four nodes while descending). We cast away constness in order to change the node.
current->insert(new_key, value);
++tree_size;
}
/*
* Called by insert(Key key, const Value& value) to determine if key exits or not.
* Precondition: pnode is never nullptr.
*
* Purpose: Recursive method that searches the tree for 'new_key', splitting 4-nodes when encountered. If key is not found, the tree descent terminates at
* the leaf node where the new 'new_key' should be inserted, and it returns the pair {false, pnode_leaf_where_key_should_be_inserted}. If key was found,
* it returns the pair {true, Node *pnode_where_key_found}.
*/
template<class Key, class Value> std::tuple<bool, typename tree234<Key, Value>::Node *, int> tree234<Key, Value>::find_insert_node(Node *pcurrent, Key new_key) noexcept
{
if (pcurrent->isFourNode()) {
if (pcurrent->key(1) == new_key) // First check the middle key because split() will move it into its parent.
return {true, pcurrent, 1};
// split pcurrent into two 2-nodes and set pcurrent to the Node to examine next(int the loop below).
pcurrent = split(pcurrent, new_key);
}
auto i = 0;
for(; i < pcurrent->getTotalItems(); ++i) {
if (new_key < pcurrent->key(i)) {
if (pcurrent->isLeaf())
return {false, pcurrent, i};
return find_insert_node(pcurrent->children[i].get(), new_key); // Recurse left subtree of pcurrent->key(i)
}
if (new_key == pcurrent->key(i)) {
return {true, pcurrent, i}; // key located at std::pair{pcurrent, i};
}
}
if (pcurrent->isLeaf()) {
return {false, pcurrent, 0};
}
return find_insert_node(pcurrent->children[i].get(), new_key); // key is greater than all values in pcurrent, search right-most subtree.
}
/*
* split pseudocode:
*
* Input: pnode is a 4-node that is is split follows:
* Output:
* 1. A new 2-node containing pnode's largest key(the 3rd key) is created, it adopts pnode's two right-most children.
* 2. pnode is downsized to a 2-node (by setting totalItems to 1) containing its smallest key and its two left-most chidren,
* 3. pnode's middle key moves up to its parent (which we know is not a 4-node, since, if it were, it has already been split), and we connect the new
* 2-node step from #1 to it as its right most child.
*
* Special case: if pnode is the root, we special case this and create a new root above the current root.
*
*/
template<typename Key, typename Value> typename tree234<Key, Value>::Node *tree234<Key, Value>::split(Node *pnode, Key new_key) noexcept
{
Key middle_key = pnode->key(1);
// 1. create a new node from largest key of pnode and adopt pnode's two right-most children
auto largestNode = std::make_unique<Node>(std::move(pnode->keys_values[2]));
largestNode->connectChild(0, pnode->children[2]);
largestNode->connectChild(1, pnode->children[3]);
// 2. Make pnode a 2-node by setting totalItmes. Note: It still retains its two left-most children,
pnode->totalItems = 1;
Node *pLargest = largestNode.get();
// 3. Insert middle value into parent, or if pnode is the root, create a new root above pnode and
// adopt 'pnode' and 'largest' as children.
if (root.get() == pnode) {
auto new_root = std::make_unique<Node>(std::move(pnode->keys_values[1])); // Middle value will become new root
new_root->connectChild(0, root);
new_root->connectChild(1, largestNode);
// Since root was moved above, we can safely move into it.
root = std::move(new_root);
} else {
// Insert pnode's keys_values[1] into its parent, and makes largestNode its child.
pnode->parent->insert(std::move(pnode->keys_values[1]), largestNode);
}
// Set pnext. Since we already checked 'if (new_key == middle_key)' in the caller--in find_insert_node()--we need only check if 'new_key < middle_key', in order to set pnext to the node
// for find_insert_node() to examine next.
Node *pnext = (new_key < middle_key) ? pnode : pLargest;
return pnext;
}
/*
* Converts 2-nodes to 3- or 4-nodes as it descends to the left-most leaf node of the substree rooted at pnode.
* Returns: min leaf node in subtree rooted at pnode.
*/
template<class Key, class Value> inline typename tree234<Key, Value>::Node *tree234<Key, Value>::get_successor_node(Node *pnode, int child_index) noexcept
{
if (pnode->isTwoNode())
convert2Node(pnode, child_index);
if (pnode->isLeaf())
return pnode;
return get_successor_node(pnode->children[0].get(), 0);
}
template<typename Key, typename Value> inline void tree234<Key, Value>::printlevelOrder(std::ostream& ostr) const noexcept
{
NodeLevelOrderPrinter tree_printer(height(), (&Node::print), ostr);
levelOrderTraverse(tree_printer);
ostr << std::flush;
}
template<typename Key, typename Value> void tree234<Key, Value>::debug_printlevelOrder(std::ostream& ostr) const noexcept
{
ostr << "\n--- First: tree printed ---\n";
ostr << *this; // calls tree.printlevelOrder(ostr);
ostr << "\n--- Second: Node relationship info ---\n";
NodeLevelOrderPrinter tree_printer(height(), &Node::debug_print, ostr);
levelOrderTraverse(tree_printer);
ostr << std::flush;
}
template<typename Key, typename Value> inline void tree234<Key, Value>::printInOrder(std::ostream& ostr) const noexcept
{
auto lambda = [&](const std::pair<Key, Value>& pr) { ostr << pr.first << ' '; };
inOrderTraverse(lambda);
}
template<class Key, class Value> tree234<Key, Value>::iterator::iterator(tree234<Key, Value>& lhs_tree) : tree{lhs_tree}
{
current = (!tree.isEmpty()) ? get_min() : nullptr;
cursor = current;
key_index = 0;
}
template<class Key, class Value> std::ostream& tree234<Key, Value>::iterator::print(std::ostream& ostr) const noexcept
{
ostr << "\n-------------------------------------\niterator settings:\ncurrent = " <<\
current << "\n" << "cursor = " << cursor << '\n';
ostr << *cursor; // print the node
ostr << "\nkey_index = " << key_index << '\n';
ostr << "stack = { ";
std::deque<int> deque;
//tree234<Key, Value>::iterator& nonconst = const_cast<iterator&>(*this);
tree234<int, int>::iterator& non_const = const_cast<tree234<Key, Value>::iterator&>(*this);
while(!non_const.child_indexes.empty()) {
auto top = non_const.child_indexes.top();
ostr << top << ", ";
deque.push_back(top);
non_const.child_indexes.pop();
}
ostr << " } " << '\n' << std::flush;
// Push elements back onto stack in opposite order they were pop()'ed
while(!deque.empty()) {
int i = deque.back();
non_const.child_indexes.push(i);
deque.pop_back();
}
return ostr;
}
template<typename Key, typename Value> inline const typename tree234<Key, Value>::Node *tree234<Key, Value>::iterator::get_max() noexcept
{
const Node *pnode = tree.root.get();
for (auto child_index = pnode->getTotalItems(); pnode->children[child_index]; child_index = pnode->getTotalItems()) {
push(child_index);
pnode = pnode->children[child_index].get();
}
return pnode;
}
template<typename Key, typename Value> inline const typename tree234<Key, Value>::Node *tree234<Key, Value>::iterator::get_min() noexcept
{
const Node *pnode = tree.root.get();
for(auto child_index = 0; pnode->children[child_index].get(); pnode = pnode->children[child_index].get()) {
push(child_index);
}
return pnode;
}
// non const tree234<Key, Value>& passed to ctor. Called only by end()
template<class Key, class Value> inline tree234<Key, Value>::iterator::iterator(tree234<Key, Value>& lhs_tree, int i) : tree{lhs_tree}
{
// If the tree is empty, there is nothing over which to iterate...
if (!tree.isEmpty()) {
cursor = get_max(); // Go to largest node.
key_index = cursor->get_lastkey_index();
current = nullptr;
} else {
cursor = current = nullptr;
key_index = 0;
}
}
template<class Key, class Value> inline typename tree234<Key, Value>::iterator tree234<Key, Value>::begin() noexcept
{
return iterator{*this};
}
template<class Key, class Value> inline typename tree234<Key, Value>::const_iterator tree234<Key, Value>::begin() const noexcept
{
return const_iterator{*this};
}
template<class Key, class Value> inline typename tree234<Key, Value>::iterator tree234<Key, Value>::end() noexcept
{
return iterator(const_cast<tree234<Key, Value>&>(*this), 0);
}
template<class Key, class Value> inline typename tree234<Key, Value>::const_iterator tree234<Key, Value>::end() const noexcept
{
return const_iterator(const_cast<tree234<Key, Value>&>(*this), 0);
}
template<class Key, class Value> inline typename tree234<Key, Value>::reverse_iterator tree234<Key, Value>::rbegin() noexcept
{
return reverse_iterator{ end() };
}
template<class Key, class Value> inline typename tree234<Key, Value>::const_reverse_iterator tree234<Key, Value>::rbegin() const noexcept
{
return const_reverse_iterator{ end() };
}
template<class Key, class Value> inline typename tree234<Key, Value>::reverse_iterator tree234<Key, Value>::rend() noexcept
{
return reverse_iterator{ begin() };
}
template<class Key, class Value> inline typename tree234<Key, Value>::const_reverse_iterator tree234<Key, Value>::rend() const noexcept
{
return const_reverse_iterator{ begin() };
}
template<class Key, class Value> typename tree234<Key, Value>::iterator& tree234<Key, Value>::iterator::increment() noexcept
{
if (tree.isEmpty()) {
return *this; // If tree is empty or we are at the end, do nothing.
}
auto [successor, index] = getSuccessor(cursor, key_index);
if (!successor) { // nullptr implies cursor->keys_values[key_index].key() is the max key,
// the last key/value in tree.
current = nullptr; // We are now at the end.
} else {
cursor = current = successor;
key_index = index;
}
return *this;
}
template<class Key, class Value> typename tree234<Key, Value>::iterator& tree234<Key, Value>::iterator::decrement() noexcept
{
if (tree.isEmpty()) {
return *this;
}
if (!current) { // If already at the end, then simply return the cached value and don't call getPredecessor()
current = cursor;
return *this;
}
auto [predecessor, index] = getPredecessor(cursor, key_index);
if (predecessor) { // nullptr implies there is no predecessor cursor->key(key_index).
cursor = current = predecessor;
key_index = index;
} else {
current = nullptr;
}
return *this;
}
template<class Key, class Value> inline tree234<Key, Value>::iterator::iterator(iterator&& lhs) : \
tree{lhs.tree}, current{lhs.current}, cursor{lhs.cursor}, key_index{lhs.key_index}
{
lhs.cursor = lhs.current = nullptr;
child_indexes = std::move(lhs.child_indexes);
}
/*
*/
template<class Key, class Value> bool tree234<Key, Value>::iterator::operator==(const iterator& lhs) const
{
//
// The first if-test, checks for "at end".
// If current is nullptr, that signals the iterator is "one past the end.". If current is not nullptr, then current will equal cursor.current is either nullptr or cursor. cursor never
// becomes nullptr.
// In the else-if block block, we must check 'current == lhs.current' and not 'cursor == lhs.cursor' because 'cursor' never signals the end of the range, it never becomes nullptr,
// but the iterator returned by tree234::end()'s iterator always sets current to nullptr (to signal "one past the end").
// current to nullptr.
//
// TODO: Does this logic properly hand reverse iterators, too, even when they are empty?
if (!current && !lhs.current) return true;
else if (current == lhs.current && key_index == lhs.key_index) {
return true;
} else return false;
}
/*
tree234<Key, Value>::const_iterator constructors
*/
template<class Key, class Value> inline tree234<Key, Value>::const_iterator::const_iterator(const tree234<Key, Value>& lhs) : iter{const_cast<tree234<Key, Value>&>(lhs)}
{
}
template<class Key, class Value> inline tree234<Key, Value>::const_iterator::const_iterator(const tree234<Key, Value>& lhs, int i) : iter{const_cast<tree234<Key, Value>&>(lhs), i}
{
}
template<class Key, class Value> inline tree234<Key, Value>::const_iterator::const_iterator::const_iterator(const typename tree234<Key, Value>::const_iterator& lhs) : iter{lhs.iter}
{
}
template<class Key, class Value> inline tree234<Key, Value>::const_iterator::const_iterator::const_iterator(typename tree234<Key, Value>::const_iterator&& lhs) : iter{std::move(lhs.iter)}
{
}
/*
* This constructor also provides implicit type conversion from a iterator to a const_iterator
*/
template<class Key, class Value> inline tree234<Key, Value>::const_iterator::const_iterator::const_iterator(const typename tree234<Key, Value>::iterator& lhs) : iter{lhs}
{
}
template<class Key, class Value> inline bool tree234<Key, Value>::const_iterator::operator==(const const_iterator& lhs) const
{
return iter.operator==(lhs.iter);
}
template<class Key, class Value> inline bool tree234<Key, Value>::const_iterator::operator!=(const const_iterator& lhs) const
{
return iter.operator!=(lhs.iter);
}
/*
* Returns -1 is pnode not in tree
* Returns: 0 for root
* 1 for level immediately below root
* 2 for level immediately below level 1
* 3 for level immediately below level 2
* etc.
*/
template<class Key, class Value> int tree234<Key, Value>::depth(const Node *pnode) const noexcept
{
if (!pnode) return -1;
int depth = 0;
for (const Node *current = root; current; ++depth) {
if (current->key() == pnode->key()) {
return depth;
} else if (pnode->key() < current->key()) {
current = current->left;
} else {
current = current->right;
}
}
return -1; // not found
}
template<class Key, class Value> int tree234<Key, Value>::height(const Node* pnode) const noexcept
{
if (!pnode) {
return -1;
} else {
std::array<int, 4> heights;
int num_children = pnode->getChildCount();
// Get the max height of each child subtree.
for (auto i = 0; i < num_children; ++i) {
heights[i] = height(pnode->children[i].get());
}
int max = *std::max_element(heights.begin(), heights.begin() + num_children);
return 1 + max; // add one to it.
}
}
/*
Input: pnode must be in tree
*/
template<class Key, class Value> bool tree234<Key, Value>::isBalanced(const Node* pnode) const noexcept
{
if (!pnode) return false;
std::array<int, 4> heights; // four is max number of children.
int child_num = pnode->getChildCount();
for (auto i = 0; i < child_num; ++i) {
heights[i] = height(pnode->children[i].get());
}
int minHeight = *std::min_element(heights.begin(), heights.begin() + child_num);
int maxHeight = *std::max_element(heights.begin(), heights.begin() + child_num);
// Get absolute value of difference between max height and min of height of children.
int diff = std::abs(maxHeight - minHeight);
return (diff == 1 || diff ==0) ? true : false; // return true if absolute value is 0 or 1.
}
// Visits each Node in level order, testing whether it is balanced. Returns false if any node is not balanced.
template<class Key, class Value> bool tree234<Key, Value>::isBalanced() const noexcept
{
if (root ==nullptr) return true;
std::queue<const Node *> nodes;
nodes.push(root.get());
while (!nodes.empty()) {
const Node *current = nodes.front();
nodes.pop(); // remove first element
if (isBalanced(current) == false) return false;
// push its children onto the stack
for (auto i = 0; i < current->getChildCount(); ++i) {
if (current->children[i]) {
nodes.push(current->children[i].get());
}
}
}
return true; // All Nodes were balanced.
}
#endif